Choices for the f function

Before settling on the final choice of f as described in Eq. (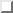) three separate forms were experimented with.

1. A spherical f function that was cut off by a Fermi function at the edge of the largest sphere that could be inscribed within the Wigner-Seitz cell, i.e.

   

   where is the radius of the above sphere. This function was thought at the time to be more elegant as it removed any discontinuity in the gradient of f as an electron moves out of one side of the simulation cell and back in the opposite side.

2. A spherical f function with a sharp cut off at the edge of the largest sphere that could be inscribed within the Wigner-Seitz cell, i.e.

   

3. The f function described by Eq. (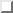), which is not spherically symmetrical, and has a sharp cut off at the edge of the Wigner-Seitz cell.

Hartree-Fock calculations using LDA orbitals and VMC calculations showed that for the larger simulation cells, n=3,4,5 the energies obtained from all 3 interactions were virtually identical. For the smallest system size (n=2), the total energy was reduced by choosing the interaction, (iii), of Eq. (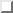). This is to be expected as the extra regions outside the cutoff sphere in this interaction allow more correlation between electrons. This choice of f also preserves the sum rule in the interaction of each electron with its exchange-correlation hole, i.e. each electron is interacting with the whole of the exchange-correlation hole via the 1/r interaction. If f is chopped off before the edge of the Wigner-Seitz cell as in (i) and (ii), then each electron does not interact via 1/r with the whole of the exchange-correlation hole.

The discontinuity in the derivative of the interaction introduced by this choice of f only introduces a discontinuity into the third derivative of the exact wavefunction. This does not contribute to the kinetic energy of the system and is therefore harmless.