Next: Usage
Up: Module constraints_module
Previous: Module constraints_module
Contents
Index
Contains the Constraint type and constraint subroutines
Constraints are applied using the RATTLE algorithm:
H. C. Andersen, JCompPhys 52 24-34 (1983)
This itself is based on the SHAKE algorithm:
J. P. Ryckaert et al., JCompPhys 23 327-341 (1977)
To integrate the system with constraints Newtons equations of motion have to be modified to
where 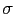 is a constraint function (see below) and
is a constraint function (see below) and
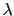 is a Lagrange multiplier which is dependent upon atomic positions
and velocities.
is a Lagrange multiplier which is dependent upon atomic positions
and velocities.
When the equations of motion are discretised two separate approximation to 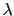 must be
made so that the positions and velocities both obey the constraint exactly (or to within a
specified precision) at each time step.
must be
made so that the positions and velocities both obey the constraint exactly (or to within a
specified precision) at each time step.
During the position updates, a Lagrange multiplier 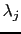 attached to a constraint
attached to a constraint
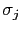 , which involves particles
, which involves particles 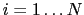 is solved for iteratively by the following:
is solved for iteratively by the following:
The velocity updates also include the
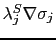 term, plus an additional
term, plus an additional
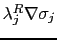 term where
term where 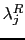 is solved for via:
is solved for via:
The full, non-specialised form of the iterative solver is present in the code for added flexibility and
to allow users to write and use their own constraint functions, which can be time dependent.
Writing extra constraint subroutines
A constraint subroutine evaluates a constraint function (C), its derivatives with respect to all
coordinates (dC_dr) and its full time derivative (dC_dt). A constraint function is a function which
evaluates to zero when the constraint is satisfied.
Probably the easiest way of constructing a new subroutine is to copy the following and fill in the gaps:
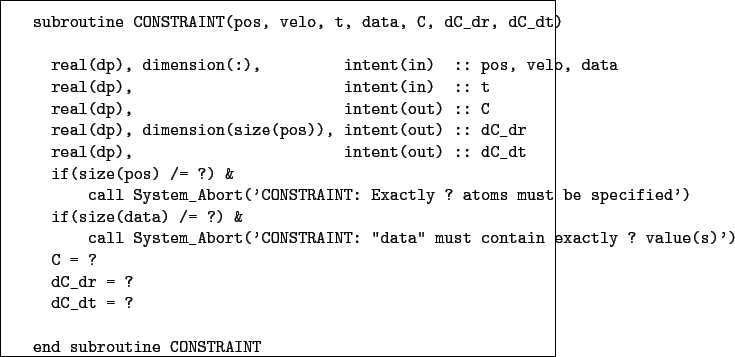
A few notes:
- The subroutine must make its own checks on the sizes of the input arguments (as shown)
- dC_dr should not be zero when the constraint is satisfied, since then no force can be applied to
enforce the constraint. For example, the plane constraint could have been defined as the squared
distance from the plane, but that would cause it to suffer from this problem, so the signed
distance was used instead.
- Currently, a constraint function can only depend explicitly on positions and time, so the kinetic
energy of a group of particles cannot be constrained for example.
- dC_dt will usually be dC_dr .dot. velo, except in the case where the constraint depends explicitly
on time; then there will be an extra partial d/dt term.
- If a constraint contains one particle only, then the absolute position of that particle is passed
in pos. If more than one particle is in the constraint then the relative positions are passed
(with the first particle at the origin), so periodic boundary conditions should not be a worry.
- When a constraint is added to a DynamicalSystem its number of degrees of freedom is decreased by 1.
A constraint should only attempt to remove one degree of freedom MAXIMUM. Constraints which try to,
for examples, keep a particle on a line (removing 2 degrees of freedom) are doomed to failure since
the particle will not always be able to return to the line by the application of forces in the direction
from the particle to the nearest point on the line. Instead, implement the line as the intersection of
two planes, which makes the removal of two degrees of freedom more explicit, and allows the algorithm
to use two directions to construct the constraint force.
- Some constraints will be extraneous (e.g. constraining a bond length which, by the action of many
other constraints, is already fixed implicitly), and the decrease of ds%Ndof will be wrong, in which
case it should be correctly set by hand. Also, the algorithm will fail if the explicit constraint
is not the same as the implicit one.





Next: Usage
Up: Module constraints_module
Previous: Module constraints_module
Contents
Index
gabor
2009-06-30
![]() must be
made so that the positions and velocities both obey the constraint exactly (or to within a
specified precision) at each time step.
must be
made so that the positions and velocities both obey the constraint exactly (or to within a
specified precision) at each time step.
![]() attached to a constraint
attached to a constraint
![]() , which involves particles
, which involves particles ![]() is solved for iteratively by the following:
is solved for iteratively by the following:
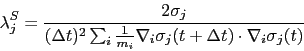
![]() term, plus an additional
term, plus an additional
![]() term where
term where ![]() is solved for via:
is solved for via: