Subroutine find_motif

Subgraph isomorphism identifier based on J.R. Ullmann, JACM 23(1) 31-42 (1976)

Slight modifications are that if we include two unconnected vertices in the subgraph then the corresponding vertices in the isomorphism MUST also be disconnected. i.e. if we don't include a bond between two atoms it is because it really isn't there.

Pattern matching problems are combinatorial in time required, so the routine itself has seven different escape routes; the first six try to quickly fail and prevent the main part of the algorithm from executing at all.

at is the atoms structure with connectivity data precalculated to at least first nearest neighbours

motif is an integer matrix describing the connectivity of the region you wish to match. it has dimension (number of atoms, max number of neighbours + 1) motif(i,1) is the atomic number of an atom motif(i,2), motif(i,3) etc. are the indices of atoms to which this atom connects in this motif or zero if there are no more neighbours.

E.g. to match a water molecule we could use:

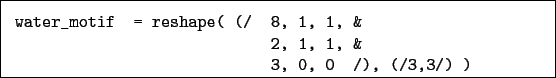
or, alternatively:

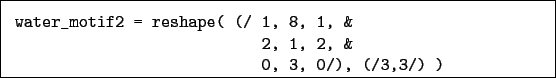
and for an alpha carbon

The routine will identify an optimum atom in the motif which it will try to find in the atoms structure before doing any further matching. The optimum atom is the one which minimises the total number of bond hops required to include all atoms in the motif

matches is a table containing one line for each match found in the atoms structure or for optimum atoms with indices between start and end. The integers in each line give the indices of the atoms, in the same order as in the motif, which consitute a single match.

mask allows individual atoms to be selected for searching, e.g. for preventing a water molecule from being re-identified as an OH, and then later as two hydrogens.

at -- type(atoms), intent(in)

The atoms structure to search

motif -- integer, intent(in), dimension(:,:)

The motif to search for

matches -- type(table), intent(out)

All matches

start, end -- integer, optional, intent(in)

Start and End atomic indices for search

mask -- logical, optional, intent(in), dimension(:)

If present only masked atoms are searched

Graphene_Cubic function