Position Operator
We follow the analysis of Stengal and Spaldin: They show that for gamma point sampling a finite-difference k-space representation of the position operator corresponds to replacing the true linear position operator with a sin function in the unit cell (the position operator is centred at the geometric centre of each Wannier Function). Using a mesh of kpoints in the BZ corresponds to a position operator periodic in a supercell of the unit cell. The generalisation of their formula to 3D and a set of b-vectors is
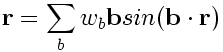
By comparing this position operator in real space with the true operator we can again some insight to the approximations involved. (there is a equivalent expression for the spread operator). There are two issues; first the convergence with supercell size, or equivalently the convergence with the density of k-space sampling. Secondly the asymmetry introduced by the discretisation, (the true position operator is spherically symmetric). Note that if the b-vectors are from a complete shell of kpoints then they are closed under the point-group operations and the above position operator will transform. There are lots of measures one could plot, I've looked at the following
- pos_op The spherically averaged magnitude of the position operator
- rms error The spherical average of the rms error of the position operator with respect to its average value (ie a measure of how spherical the position operator is, not how much it differs from the true value).
- max error The maximum deviation from the average value