


Next: 2. Formulation of the
Up: Preconditioned conjugate gradient method
Previous: Preconditioned conjugate gradient method
Linear-scaling electronic structure methods [1] are
essential for calculations of large systems containing many atoms.
One of the criteria for the success of such methods is the use of a
high quality localized basis set, which is usually non-orthogonal.
Using such a basis set, one can formulate the electronic structure
problem as a generalized eigenvalue problem
 [2,3,4], which also arises naturally
in many other scientific disciplines. The properties of
[2,3,4], which also arises naturally
in many other scientific disciplines. The properties of  and
and  are that they are
are that they are  Hermitian matrices and that
Hermitian matrices and that  is
also positive definite. For the case where only the lowest few
eigenvalue-eigenvector pairs of large
is
also positive definite. For the case where only the lowest few
eigenvalue-eigenvector pairs of large 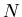 matrices are required, most
direct diagonalization (e.g. Cholesky-Householder procedure) methods
which use similarity transformations
[2,3,4,5] are inefficient
because all eigenvalue-eigenvector pairs are found. The computational
effort scales as
matrices are required, most
direct diagonalization (e.g. Cholesky-Householder procedure) methods
which use similarity transformations
[2,3,4,5] are inefficient
because all eigenvalue-eigenvector pairs are found. The computational
effort scales as 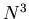 , where
, where 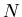 is the number of basis functions in
the calculation. Iterative methods which concentrate on only the
lowest few eigenvalue-eigenvector pairs are much more efficient
[6,7,8,9,10,11],
and are widely used to solve the standard symmetric eigenvalue
problem. Iterative solution of the generalized eigenvalue problem
usually proceeds by first performing a Cholesky decomposition of
is the number of basis functions in
the calculation. Iterative methods which concentrate on only the
lowest few eigenvalue-eigenvector pairs are much more efficient
[6,7,8,9,10,11],
and are widely used to solve the standard symmetric eigenvalue
problem. Iterative solution of the generalized eigenvalue problem
usually proceeds by first performing a Cholesky decomposition of  to obtain a standard symmetric eigenvalue problem. However, in this
work the generalized problem, cast into variational form, is solved by
the conjugate gradient method without first transforming to symmetric
form. The gradient method was proposed long ago by Hestenes and
Karush [12,13] to solve the eigenvalue
problem, where they used a steepest descent method to perform the
minimization.
to obtain a standard symmetric eigenvalue problem. However, in this
work the generalized problem, cast into variational form, is solved by
the conjugate gradient method without first transforming to symmetric
form. The gradient method was proposed long ago by Hestenes and
Karush [12,13] to solve the eigenvalue
problem, where they used a steepest descent method to perform the
minimization.
In this work, we first present an example of a generalized
eigenvalue problem taken from first-principles electronic structure
calculations. An iterative conjugate gradient minimization method
which finds the lowest few eigenvalues and eigenvectors is then
introduced. Although this method can be used for Hermitian  and
Hermitian-positive-definite
and
Hermitian-positive-definite  , it will be most efficient when
, it will be most efficient when  and
and  are also sparse, a case which arises when large systems are
studied with localized basis sets. We have taken the tensor nature of
the search direction and other quantities into account. A
preconditioning scheme related to that discussed by Bowler and Gillan
in a previous Communication [14] to improve the
convergence is proposed. To test the method we use a localized
spherical-wave basis set introduced in another Communication
[15] to perform first-principles calculations. Test cases
are taken from the molecular chlorine and bulk silicon systems. The
rate of convergence of the solutions is one of our main concerns here.
Linear convergence of the solution is observed from the results of
calculations.
are also sparse, a case which arises when large systems are
studied with localized basis sets. We have taken the tensor nature of
the search direction and other quantities into account. A
preconditioning scheme related to that discussed by Bowler and Gillan
in a previous Communication [14] to improve the
convergence is proposed. To test the method we use a localized
spherical-wave basis set introduced in another Communication
[15] to perform first-principles calculations. Test cases
are taken from the molecular chlorine and bulk silicon systems. The
rate of convergence of the solutions is one of our main concerns here.
Linear convergence of the solution is observed from the results of
calculations.



Next: 2. Formulation of the
Up: Preconditioned conjugate gradient method
Previous: Preconditioned conjugate gradient method
Peter Haynes
![]() and
Hermitian-positive-definite
and
Hermitian-positive-definite ![]() , it will be most efficient when
, it will be most efficient when ![]() and
and ![]() are also sparse, a case which arises when large systems are
studied with localized basis sets. We have taken the tensor nature of
the search direction and other quantities into account. A
preconditioning scheme related to that discussed by Bowler and Gillan
in a previous Communication [14] to improve the
convergence is proposed. To test the method we use a localized
spherical-wave basis set introduced in another Communication
[15] to perform first-principles calculations. Test cases
are taken from the molecular chlorine and bulk silicon systems. The
rate of convergence of the solutions is one of our main concerns here.
Linear convergence of the solution is observed from the results of
calculations.
are also sparse, a case which arises when large systems are
studied with localized basis sets. We have taken the tensor nature of
the search direction and other quantities into account. A
preconditioning scheme related to that discussed by Bowler and Gillan
in a previous Communication [14] to improve the
convergence is proposed. To test the method we use a localized
spherical-wave basis set introduced in another Communication
[15] to perform first-principles calculations. Test cases
are taken from the molecular chlorine and bulk silicon systems. The
rate of convergence of the solutions is one of our main concerns here.
Linear convergence of the solution is observed from the results of
calculations.