Non-linear optical properties

The development of highly efficient non-linear optical (NLO) crystals is of great importance to extending the frequency range provided by conventional laser sources into the ultraviolet and infrared regions. Therefore, the search for new NLO crystals is very active. There is a number of sometimes conflicting requirements for good NLO materials: large second harmonic generation (SHG) coefficients, a wide transparent and phase matchable region, good optical quality, and a high damage threshold. Computational screening of possible NLO materials has potential for generating good candidate crystals, and study of known NLO systems is useful for understanding the fundamental reasons for their good performance.

The prerequisite in searches for NLO materials is the ability to calculate both linear (refractive index, n) and nonlinear (second harmonic generation coefficient, SHG) optical properties that are related to second order susceptibility χ⁽²⁾. The early formalism for calculating the static limit of χ⁽²⁾ using CASTEP methodology is described and applied by Lin et al. (1999). A number of applications where SHG coefficients d_ij were calculated using CASTEP are cited in a review by Milman et al. (2010).

For small electric fields the dielectric polarization density (P) can be expressed as a Taylor expansion in terms of the electric field (E):

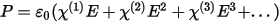
Here, we assume the polarization is instantaneous and lossless, satisfying the Kramers-Kronig constraints. The linear polarizability χ⁽¹⁾ is related to the dielectric permittivity, discussed above.

In principle, the second order polarizability χ⁽²⁾ is non-zero for any material without inversion symmetry and gives rise to 3-wave-mixing phenomena. It is a rank-3 tensor quantity related to the third derivative of the total energy with respect to electric field. These third order derivative quantities are computed in CASTEP using the 2n+1 theorem of the Density Functional Perturbation Theory following the method of Miwa (2011), also used for DFPT Raman calculations. The CASTEP implementation includes neither the phonon contribution, nor the frequency-dependence for energies above the bandgap, which modify the response at infrared and ultraviolet regions of the spectrum respectively, and therefore is appropriate for the visible optical range.

For a material where the susceptibility is dispersionless, the Kleinman symmetry condition is satisfied. This allows a contraction of the 27-element χ⁽²⁾ tensor into an 18-element tensor, d, that is symmetric in its last two indices:

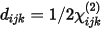
Using the following contraction, we define d_il.

jk	11	22	33	23, 32	31, 13	12, 21
l	1	2	3	4	5	6

Depending on the space group of the crystal, there are at most 10 symmetry-distinct elements of the d matrix.

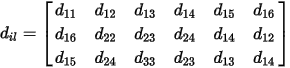
Measured quantities are most often reported in picometers per Volt, (pm/V). The book by Boyd (2003) contains more detailed background and discussion.

See Also:

Theory in CASTEP